SATÉLITES DE JUPITER

El cálculo de la posición de los satélites Galileanos de Júpiter debería se en principio sencillo pues giran en órbitas casi circulares alrededor de Júpiter y están prácticamente en el plano ecuatorial de Júpiter, por lo que los satélites se ven desde la Tierra moverse como en una línea y su movimiento es similar al movimiento vibratorio armónico, pero hay varias complicaciones: Su órbita no está exactamente en el plano ecuatorial, además la Tierra y Júpiter se mueven y la dirección Tierra-Júpiter que señalaría la conjunción superior geocéntrica o los 180º del satélite, tal como se ve desde la Tierra, varían y no lo hacen de modo uniforme.
El Sol y la Tierra forman vistos desde Júpiter un ángulo PS o ángulo de fase y por tanto el cono de sombra del planeta forma este ángulo con la dirección Tierra-Júpiter y esto determina los eclipses o los pasos de las sombras por el disco del planeta.
Para complicarlo más la luz no se propaga instantáneamente y dado que la distancia de la Tierra a Júpiter cambia los satélites parecen atrasarse o adelantarse.

El applet de Java Medici3

El applet Medici3 calcula la posición de los satélites al ingresar el día, mes, año y hora, y también si el satélite sufre algún fenómeno.

Explicación del Medici3

El applet calcula la fecha juliana y los días transcurridos desde 1900.0 que se representaran por DJ.

Angulo G

La Tierra avanza en su órbita heliocéntrica 360/365.2422= 0.985647°/día pero Júpiter avanza diariamente 360/4332.59= 0.08309 °/día por lo que el avance neto es 0.90256. El ángulo es G=0 cuando Sol, Tierra y Júpiter están alineados es decir el día de la oposición. Así pues G=0.90256*días transcurridos desde la oposición. Es fácil calcular cuando ocurrirá la siguiente oposición 360/0.90256=398.88 días lo que se conoce como periodo Sinódico. Es fundamental el día del año en que ocurre la oposición, para ver el aspecto del planeta, su sombra, y la posición de los satélites respecto a esta.

Movimientos medios

Los planetas no se mueven uniformemente alrededor del Sol sino siguiendo la ley de las áreas, sin embargo parece adecuado hablar de las anomalías medias y corregir posteriormente las diferencias con el movimiento real, anomalías verdaderas, mediante la Ecuación de Centro.
Así la longitud media de la Tierra:
M=358.476+0.9856003*DJ
Sin embargo para Júpiter y Saturno hay cierta complicación adicional. Los planetas de gran masa mantienen una órbita resonante. Cada 5 órbitas de Júpiter (aproximadamente 60 años) 5x4332,6 días=21663 días, Saturno da 2 vueltas al Sol 2x10759,24 días = 21518,5 días.
Definimos el parámetro P=237º,47555+3034º,9061.T donde T son los siglos julianos de 36525 días desde 0 de Enero de 1900 y el movimiento medio es el de Júpiter en un siglo.
Análogamente para Saturno Q=265º,91650+1222º,1139.T y el movimiento medio es el de Saturno en un siglo. La atracción mutua entre Júpiter y Saturno tiene un parámetro idóneo que es V=5.Q-2.P=134º,6314+40º,7573.T o en días desde 0 Enero de 1900:
V=134.63+1.11587E-3 *DJ
La longitud media de Júpiter está afectada por Saturno:
N=225.328+0.0830853*DJ+0.33 sen V
El ángulo TSJ también, dado que si el movimiento medio de Júpiter aumenta, el ángulo Tierra Júpiter visto desde el Sol, disminuye:
G=221.647+0.9025179*DJ-0.33 sen V

Posición heliocéntrica

La Ecuación de Centro por el movimiento elíptico viene dado por:
C=A. Verdadera- A. Media=2e. sen M+5/4 e².sen 2M
Siendo e la excentricidad y M la anomalía media.
Para la Tierra y Júpiter las Ecuaciones de centro valen:
A=1.916 sen M +0.02 sen(2M)
B=5.552 sen N +0.167sen(2N)
La razón de los factores escriba en que hay que multiplicar por RAD=180/pi =57,29577951 para convertir los radianes a grados.
Así para la Tierra e=0,01673 tenemos:
2.e=57,29577951 . 2 . 0,01673=1,917116
5e²/4=57,29577951 . 5 .0,01673²/4=0,020045
Así para Júpiter e=0,048417 tenemos:
2.e=57,29577951 . 2 . 0,048417=5,54818
5e²/4=57,29577951 . 5 .0,048417²/4=0,16789
Con lo que el ángulo verdadero TSJ es: K=G+A-B

Distancias

Las distancias heliocéntricas de la Tierra y Júpiter se pueden expresar en función del semieje a, de la excentricidad e y la anomalía media M:
R= a. (1-e. Cos M +e²/2 .(1-cos 2.M))
Así para la Tierra a=1 e=0,01673 resulta:
R=1.00014-0.01672 cos M -0.00014 cos (2M)
La razón de los coeficientes es:
Término independiente = a.(1+e²/2)=1,0001399
Primer orden =-a.e=-0,01673
Segundo orden =-a.e²/2=-0,0001399

Así para Júpiter con a=5,2028 y e=0,048417
r=5.20867-0.25192 cos N -0.0061 cos (2N)
La razón de los coeficientes es:
Término independiente = a.(1+e²/2)=5,208898
Primer orden =-a.e=-0,251904
Segundo orden =-a.e²/2=-0,006098

Se puede ahora calcular la distancia Tierra Júpiter mediante T. coseno:
DR=(R² +r² -2Rr cos K)^1/2

Corrección de tiempo de luz

La corrección por tiempo de luz se funda en que el fenómeno no se observa inmediatamente que ocurre sino que la luz necesita viajar a la Tierra. El retardo en los eclipses de Io fue usado antiguamente por Roëmer para averiguar que la luz no se transmitía inmediatamente y fue una primera medida de esta velocidad. Si DR es la distancia de la Tierra a Júpiter y c la velocidad de la luz, el retardo es DR/c.
El tiempo de luz en días es:
DR/c =DR (UA) 149.6E6/(299792x60x60x24)=DR. 5,7756E-3 =DR/173,142

Angulo de fase PS

El ángulo de fase es el ángulo que forman la Tierra y el Sol vistos desde Júpiter. Este ángulo coincide con el ángulo que forman sobre la órbita la oposición geocéntrica de un satélite y la posición de la sombra de Júpiter. Este ángulo no llega nunca a un valor de 12° dados los tamaños de las órbitas heliocéntricas de Júpiter y de la Tierra.
Efectivamente en el momento de mayor fase SEN PSmax=1/a siendo a la distancia media en UA de la órbita de Júpiter a=5.20256. Ello significa PSmax=11.0820°.

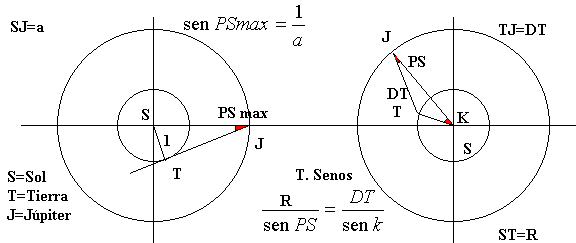
La fase o ángulo que forman vistos desde Júpiter la Tierra y el Sol se calcula mediante el teorema de los senos en el triángulo Sol-Tierra-Júpiter:
R/sen PS=DT/sen K
El ángulo de fase PS es importante pues determina el ángulo visto desde Júpiter entre la ocultación de un satélite por Júpiter y su eclipse por el cono de sombra. El ángulo PS se calcula por el arco seno y hay una ambigüedad en el signo, que se resuelve diciendo que el signo de PS es igual al signo de seno de k, siendo k=L(tierra)-L(Júpiter), longitudes heliocéntricas. El ángulo de fase es positivo tras la oposición con la sombra proyectándose al ESTE y negativo tras la conjunción con la sombra proyectándose al OESTE .
Si el instante es anterior a la oposición la longitud de la Tierra es menor que la de Júpiter y el ángulo k es negativo por lo que al aplicar el T. de los senos PS es negativo. Por el contrario, tras la oposición PS es positivo.

Conjunción superior geocéntrica

Un satélite de Júpiter está en conjunción superior geocéntrica cuando la Tierra, Júpiter y el satélite están alineados y por este orden. Es decir cuando el satélite está a mitad de la ocultación por el disco de Júpiter. Si por el contrario están alineados pero es el satélite el que ocupa la posición central, el satélite se encuentra en la conjunción inferior geocéntrica, dicho satélite se encuentra a la mitad del tránsito sobre el disco del planeta. El ángulo S(j) se mide a partir de este punto.
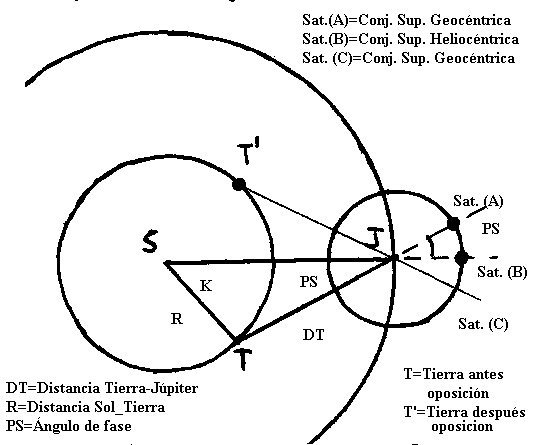
La conjunción superior heliocéntrica ocurre cuando el Sol, Júpiter y el satélite están alineados y por este orden. Es decir cuando el satélite está a mitad de un eclipse por el cono de sombra de Júpiter. Se llama periodo sinódico al lapso de tiempo entre dos conjunciones superiores heliocéntricas
Es obvio que la conjunción superior heliocéntrica ocurre cuando el satélite tiene la longitud heliocéntrica de Júpiter, mientras que la conjunción superior geocéntrica ocurre cuando el satélite tiene la longitud geocéntrica de Júpiter y que entre ambas hay una relación:
L(geocéntrica conjunción superior)=L(heliocéntrica de Júpiter)-PS siendo PS el ángulo de fase.
Por el signo de PS es cierta la relación siempre.

Longitud del satélite en su órbita

A continuación viene el cálculo de la longitud del satélite en su órbita en el instante de efemérides. Para ello figuraran como datos:
L0=longitud en la época Q (0 Enero 1900)
W= movimiento medio diario
R= radio órbita en radios Júpiter
I= Inclinación de la órbita
N= nodo de la órbita
para cada uno de los cuatro satélites.
Tras leer los datos con referencia a 1900.0, radios, y movimientos medios de los cuatro satélites calcula la longitud en la órbita y el ángulo respecto a la conjunción inferior geocéntrica de cada satélite mediante:
L(j)=L0+(w+0.0830853)(DJ-DR/173.14)
S(j)=S0+w(DJ-DR/173.14)+PS-B
donde el término DR/173.14 es el retraso que sufre la luz en llegar a la Tierra. PS es el ángulo de fase y B la ecuación de Centro para Júpiter
Para el cálculo se establece un bucle en j=1 hasta j=4. Calculado L(j) para el instante de efemérides, corrigiéndolo del tiempo de luz, se reduce al primer giro, aunque no es necesario, y posteriormente se calcula el ángulo que forma el satélite respecto a la dirección de oposición geocéntrica S(j). Para la consideración de los fenómenos si es necesario transformarlo al primer giro.

Elongación, latitud y Dirección

Ahora se puede calcular la elongación como X=R sen S.
Para la latitud del satélite habrá que tener presente que:
sen D=sen I sen (L-N) y que Y=R sen D
Un aspecto interesante es la dirección EW o WE en que se moverán los satélites. Si S pertenece { 1° o 4°} cuadrante el movimiento es de W a E -->, mientras en caso contrario el movimiento es de E a W <--.
La característica del sentido del movimiento la da el signo de COS S:
Con x<0 y movimiento --> el satélite se dirige a una ocultación o eclipse
Con x>0 y movimiento <-- el satélite se dirige a un paso o tránsito.

Así las coordenadas cartesianas del movimiento de cada satélite:
x=Rj sen S
y=Rj sen I sen(L-N)
donde I es la inclinación de cada órbita y N el nodo de la órbita.
En cuanto al sentido del movimiento se caracteriza mediante el signo del Cos S<0 significa movimiento -->.

Características del cono de sombra de Júpiter

Si rs es el radio del Sol, rj el radio de Júpiter, r la distancia heliocéntrica a Júpiter y H la altura del cono de sombra:

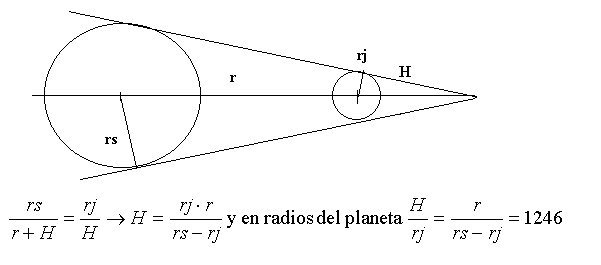
Como los satélites galileanos giran como máximo a 26 radios del planeta, el cono de sombra se puede considerar prácticamente cilíndrico para ellos.

Angulo PH de la órbita del satélite bajo la cual sufre ocultación, eclipse

Suponiendo que el cono de sombra es cilíndrico para una ocultación resulta

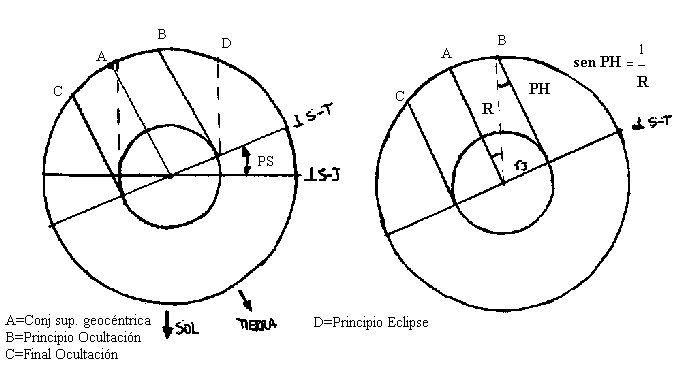
Si r es el radio al que gira el satélite expresado en radios del planeta Júpiter, se demuestra rápidamente que:
sen PH=1/R Esto equivale a alejar al infinito la posición del Sol.

CONSIDERACION DE LOS FENOMENOS.-

La variable que guardará el fenómeno es FM(j) donde j es un índice que varía entre 1 y 4.
Estudiemos ahora como tratar los distintos fenómenos:

1)TRANSITOS

Se produce si el satélite va de E a W y con una longitud geocéntrica del satélite S(j) pertenece al 3° ó 4° cuadrante y con distancia al centro del disco menor que 1. Hay que colocar en FM="Trans."

2)PASO DE LA SOMBRA

La longitud heliocéntrica variaba de la geocéntrica solo en el ángulo de fase PS y por la diferencia de signos entre antes y después de la oposición, se cumplía siempre que la longitud geocéntrica de la sombra valía S(j)-PS. Se calcula XS(j) e YS(j) habiendo paso de la sombra si la sombra dista del centro menos de 1. Habrá que colocar en FM="sombra".
Pero puede ocurrir que dos fenómenos ocurran simultáneamente, un satélite puede estar transitando sobre el disco y a su vez la sombra. El sistema consiste en ver si FM(j) esta vacía en cuyo caso no hay transito y se asigna a FM(j)="SOMBRA" pero si en FM(j)="Trans." y ocurre la sombra entonces hay que asignar FM(j)="Trans.Somb".

3)OCULTACION Y ECLIPSES

3.1 Consideremos la posición de la Tierra tras la oposición y antes de la conjunción.

Sabemos que:

a)El planeta Júpiter proyecta su sombra hacia el ESTE.
b) El ángulo de fase PS>0
c) El satélite se oculta por el W sin ser eclipsado y normalmente se eclipsa durante la ocultación. No reaparece por el E sino que sigue eclipsado apareciendo a una cierta distancia del limbo E al finalizar el eclipse.
d) Excepcionalmente para los satélites III, IV y en las épocas del año cuando abs(PS)>7.6047 para III y abs(PS)>4.3016 para IV la secuencia de fenómenos puede ser:
a) Principio de la Ocultación
b) Fin de la Ocultación
c) Principio del Eclipse
d) Fin del eclipse

Entre el Fin de la Ocultación y el Principio del Eclipse el satélite se ve al E del limbo antes de desaparecer. Para simplificar el tema se supuso que la Tierra y el Sol están en el infinito y que los conos de sombra y ocultación son cilindros. Para un satélite que diste r radios del planeta el ángulo PH de la órbita para el cual el satélite está oculto o eclipsado vale :PH=180/(pi*R(Z))

Los fenómenos ocurren a las longitudes:
a) Oc= Ocultación comienza a 180-ph
b) Ot= Ocultación termina a 180+ph
c) Ec= Eclipse comienza a 180+ps-ph
d) Et= Eclipse termina a 180+ps+ph
e)La secuencia normal de los fenómenos es:

a) Principio Ocultación =Oc que ocurre a 180-ph
b) Eclipse comienza =Ec que ocurre a 180+ps-ph
c) Ocultación termina =Ot que ocurre a 180+ph
d) Eclipse termina =Et que ocurre a 180+ps+ph

Los fenómenos en los eclipses ocurren cuando se dan las condiciones:
1)Si Ec<S(Z)<Et y siempre que abs(y)<1 el satélite está en eclipse FM(j)="Eclipse"
2)Si Oc<S(Z)<Ot y siempre que x² +y² <1 el satélite está oculto y FM$(j)="Ocult."

3.2 Consideremos la posición de la Tierra antes de la oposición y después de la conjunción.

Sabemos que:

a)El planeta Júpiter proyecta su sombra hacia el OESTE.
b) El ángulo de fase PS<0
c) El satélite se eclipsa por el W antes de ocultarse y normalmente acaba el eclipse durante la ocultación por lo que reaparece por el E junto al limbo.
d) Excepcionalmente para los satélites III, IV y en las épocas del año cuando abs(PS)>7.6047 para III y abs(PS)>4.3016 para IV la secuencia de fenómenos puede ser:
a) Principio del Eclipse
b) Fin del Eclipse
c) Principio de la Ocultación
d) Fin de la Ocultación

Entre el Fin del Eclipse y el Principio de la Ocultación el satélite se ve al W del limbo antes de desaparecer.
Teniendo presente que PS<0 los fenómenos ocurren a las longitudes:

a) Oc= Ocultación comienza a 180-ph
b) Ot= Ocultación termina a 180+ph
c) Ec= Eclipse comienza a 180+ps-ph
d) Et= Eclipse termina a 180+ps+ph
es decir las mismas condiciones que en 3.1.
e)La secuencia normal de los fenómenos es:
a) Eclipse comienza = Ec
b) Ocultación comienza =Oc
c) Eclipse termina =Et
d) Ocultación termina =Ot

Los fenómenos en los eclipses ocurren cuando se dan las condiciones:
1)Si Ec<S(j)<Et y siempre que abs(y)<1 el satélite está en eclipse FM(j)="Eclipse"
2)Si Oc<S(j)<Ot y siempre que x² +y² <1 el satélite está oculto y FM(j)="Ocult."

PRUEBAS DE FUNCIONAMIENTO DE MEDICI3

Un caso donde se demuestra el buen funcionamiento de MEDICI3 es introducir el instante 11,4,1985 a las 0h 10m en este momento el satélite I está oculto y no aparecerá hasta las 1h 58m y el satélite III está eclipsado. A las 0h 20m el satélite III que no había aparecido al W deja de estarlo apareciendo junto al borde antes de ocultarse a las 1h 46m.
Se han probado todos los fenómenos con bastantes buenos resultados, excepto los eclipses del IV pues en los años 1985-86 este fenómeno no ocurría.

APLICACION DE MEDICI3 A LAS OBSERVACIONES DE GALILEO

Los datos están tomados del libro "El mensaje y el mensajero sideral" Galileo/Kepler ED. Alianza y describe el descubrimiento de los satélites de Júpiter
Las observaciones de Galileo tienen lugar en Padua cerca de Venecia en Enero de 1610 y en ellas se cita con mucha imprecisión la hora . Así es común decir "primera hora de la noche" la ciudad esta 48 m al E de Greenwhich y el crepúsculo en Padua en Enero acaba a las 17h 38m de TU

Programa Basic con dibujo de la posición de los satélites

Hay un programa Basic que en realidad fué realizado antes del applet donde aparte de los cálculos de posición y fenómenos, se ofrece el dibujo de los satélites.